Taxane
Taxane jamac Taxaneyaal waxay waxtar joogta ah u leedahay furfurista habdhiska isle'egyada toosan. Taxanayaalka siyaale kale oo badan waa loogu shaqaysan karaa:
Taxane waa teed laydi oo ka kooban m dhinactax iyo n joogtax oo tirooyin maangal ah. Taxane waxaa aalaaba lagu muujiyaa tibixda m × n (loo akhriyo "ma, na") m waxay utaagan tahay inta dhinactax ee taxanuhu leeyahay, n waxay utaagantahay inta jogtax ee taxanuhu leeyahay. Haddii m = n, taxanaha waxaa la yiraahdaa taxane labajibbaarane ah. Taxne waxaa lagu dhex xirtaa laba bilood ama laba sakal.
Tusaalooyinka soo socda waa taxanayaal:
- 3×1
b. Taxane 3-dhinactax 1-joogtax ah
- 2×2
t. Taxane 2-dhinactax 2-joogtax.
- 1×4
j. Taxane 1-dhinactax 4-joogtax ah.
x. Taxane 2-dhinactax 4-joogtax ah.
Taxanihii hal dhinactax kaliya leh waxaa la yiraa Taxane dhinactax markuu hal joogtax kaliyana waxaa la yiraa Taxane joogtax. Ku jirayaalka mid ka mid ah waxaa la yiraa kutiirsanayaal. Taxanaha waxaa lagu magacaabaa xaraf weyn, sida B, T, J iwm. Ama sumadda B m×n, taasoo u taagnaan karta taxana kasta oo leh m-dhinactax n-joogtax. Hoos dhigga (muujiyaha) m×n wuxuu u taaganyahay aaddimaha ama ama heerka taxanaha.
Inta kutiirsan ee taxanuhu leeyahay waxaa lagu helaa m oo lagu dhuftay n. Haddaba hadaan u noqonno tusaalaha kor ku xusan, waxaan aragnaa in: taxanaha (b) uu leeyahay addimo ah: 3×1; kan (t) 2×2; kan (j) 1×4; kan (x) uu leeyahay 2×4 sidaas oo kale taxanihii ah heerka m×n wuxuu ka kooban yahay taxanayaal ah m-dhinactax iyo taxanayaal ah n-joogtax.
Taxabaha : B2×3 waa hubaal in B2×3 uu leeyahay 2 × 3 = 6 kutiirsanayaal.
B2×3 B waxay leedahay laba taxane dhinactax oo ah iyo iyo saddex taxane oo ah joogtax
- : :
Si ballaaran taxanayaalka waxaa loo isticmaalaa jabayto qoridda sidaan soo socota.
Tusaale:
Taxana guud ee heerka 2×3 waxaa loo qori karaa
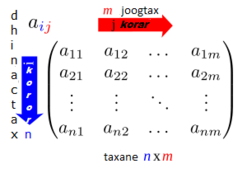
Taxana guud ee heerka m × n waxaa loo qori karaa
Waxaa loo soo gaabiyaa (a i j) marka i = (0,1,2,...m) j = (1,2,3,...n) ereyada kale ee taxanayaasha
Taxane maran. Haddii tanayaal kutiirsanayaalkiisu dhammaan yihiin, eber, taxanahaas waxaa la yiraa tanaxane maran ama taxane eber waxaa lagu asteeyaa 0 m × n.
Melmel taxane. Meelmeelka taxane B loono qoro B"" (u akhri "meelmeel B") waa taxane cusub oo ka yimid, B oo dhinactaxyadeeda la isku bedelay.
Isle'ekaanshaha taxanayaal. Laba taxane B iyo T oo isla aaddimo ah waa isle'egyihiin haddii iyo haddii qura oo kutiirsanayaashoodu isku beegani isle'egyihiin.












